Mathematicians and physicists like to name things in very silly ways. This is a great motivator: I will often read about something just because of a fun name. I’m going to try to gather some of them here, please amuse yourself! (Contrived acronyms, especially those in astronomy and machine learning to name specific projects, are excluded. They are both too common, and usually name a particular work; I am more interested in pure mathematical objects that have been named something funny.)

• Minions: 1, 2, 3. These are sets of functions $A^k \to B$ over varying $k$, which are closed under “adding a dummy argument” and “copying an argument”. Those two operations which let you increase or decrease $k$ by one, respectively. They are a weakening of a clone.
• The Eightfold Way: this system is a perspective on quantum chromodynamics (QCD) punningly named after the Eightfold Path of buddhism. The Eightfold Way is a way to organize and classify bound states of quarks, aka hadrons. Since QCD uses $SU(3)$, and $3^2-1 = 8$ counts the 3x3 matrices that aren’t the identity (1), the number 8 ocurrs a lot.
• Weft: The weft of a circuit measures how many “wide” gates are needed to keep it a low depth. The exact definition is long and somewhat clunky, but the weft turns out to nicely characterize a lot of complexity theoretic separations in the parameterized world. The term comes from the warp and weft of weaving.
• Ne: Not used seriously (yet!), but a “ne” is another name for a “co-cone”: a categorical dual of a mapping cone. In principal this term could be applied in convex optimization too, where cones are ubiquitous as is duality. This humor is in the same vein as ffee.
• Genetic, Gametic, Zygotic: These are types of algebras arising in the study of genetic populations. They are non-associative (not even power associative), but they are commutative and “third power associative”. Genetic algebras describe generally how populations multiply to produce new distributions of offspring. Gametic describes distributions of gametes in particular. Zygotic describes distribution of zygotes (two copies each) created by duplication of the gametic algebra, and further duplicating the zygotic algebra leads to the copular algebra. There is also the sex-linked zygotic algebra, which is a direct sum of male (n-dimensional) and female ($n(n+1)/2$-dimensional) algebras.
• Monogamy: The monogamy of entanglement is an important concept in quantum information that a particle A can’t be maximally entangled with B while also being maximally entangled with C. In this sense, A can only fully “marry” one of B or C. There are approximate and quantitative versions of this, and it has applications in quantum cryptography.
• Pancakes: There are pancake graphs, pancake numbers, and the pancake problem; and their “burnt” equivalent (burnt pancake graphs etc). Notably the subject of Bill Gates’ undergrad work, these are still under active research.
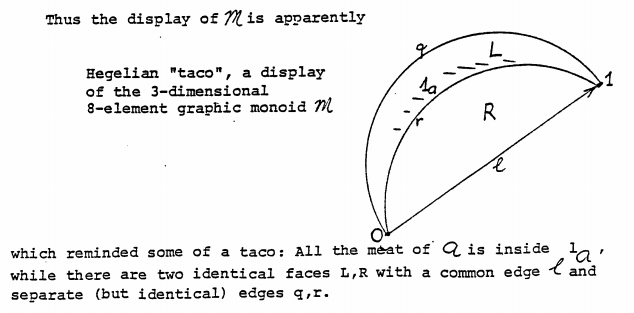
• Taco: The Hegelian taco is a particular 8-element monoid, so-named by because it looks like a taco. 🌮! The taco also happens to be a shelf; see “shelf” below.

• Quandle: A quandle is a strange little algebraic object that shows up most in knot theory. David Joyce chose the name simply to be a nonsense word that would avoid collision and confusion with existing words like “algebra” or “group”.
• Rack: Closely related to quandles, racks are a quandle without an identity. Their name, originally “wrack”, was a pun by John Conway on his colleague Gavin Wraith, and the phase wrack and ruin. Their name gave the inspiration later for shelves (next entry).
• Shelf: If you can put things on a rack, why not on a https://leanprover-community.github.io/mathlib_docs/algebra/quandle.html#shelf too? Shelves are racks that (are allowed to) lack inverses.
• Sober: A topological space is sober if it avoids certain pathological properties. Locales, an alternate way to begin axiomatizing topology, have their own pathological cases – but a topological space is a locale iff it is sober. (A locale is a topological space iff it is spatial.)
• • Pointless: By the way, the study of locales avoid an axiomatic notion of a “point”, so their study is usually called pointless topology. A more generous name is “point-free”. This is similar in spirit to the style of pointless programming, especially popular in functional programming, where individual values avoid mentioning - only functions between them.
• A Roman surface is simply named because it occurred to Jacob Steiner while he was in Rome.
• Hydra: There are hydra games and associated hydra numbers, so-called because they are described by cutting heads off a tree that lead to more heads. They are used in describing very fast-growing sequences of numbers, and probing the limits of Peano arithmetic.
• Busy Beaver: Even faster numbers arise from the Busy beaver sequence.
• Okubunions, 2023: originally studied by Okubo in 1978 and given their new name later, these are a modification of octonions that lack identity or alternativity. They may have applications in quantum chromodynamics, see also the eightfold way.
• Buildings, Apartments, and Chambers: These describe certain manifolds in an abstract form. Buildings are made out of apartments, which are in turn made out of chambers. Sometimes these are referred to as “Tits buildings” (see the “Surnames” section below).
• Clopen: Although “open” and “closed” are basic concepts in topology, they are not mutually exclusive: a set can be both open and closed at the same time. Such a set is called clopen.
• • Door: Perhaps we wish to somehow force open and closed to be opposites. It’s hard to exclude all clopen sets, as the empty set and whole space must always be clopen (this is part of the axioms of a topological space). But we can ensure that these are only two exceptions. Such a space is called connected. On the flip side, we might ask that every set is at least one of open or closed – no sets are neither one. Such spaces exist, and are called door spaces.
• HaPPY: The Happy code is a quantum error correcting code named after its authors: Daniel Harlow, Fernando Pastawski, John Preskill, Beni Yoshida. This was not the order of the names on the paper: “Fernando Pastawski, Beni Yoshida, Daniel Harlow, John Preskill”, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence. Harlow describes agonizing over the author order:

We immediately found ourselves in a quandary however: although in high-energy physics author lists are almost always alphabetical, in this case it was clear to all of us that we should acknowledge the key role played by Fernando and Beni. The problem however was that doing this would destroy one of the best author acronyms any of us had ever encountered. After agonizing about this for several weeks, we decided that in the end we simply had to feature Fernando and Beni [11]. I am glad we did. Nonetheless it was a pity to lose the acronym, so we started to use it anyways to colloquially refer to the construction: thus the HaPPY code was born.

• Monster: The Monster group is the largest sporadic simple group, sometimes known as the Friendly giant. It has a Baby monster inside it, as well as many others; the sporadic simple groups not inside are deemed Pariahs. The study of it led to Monstrous moonshine, an incredible and very deep program into mathematical symmetries of all sorts.
• • The darker version of this is umbral moonshine, where umbral means “shadowy or mysterious”. This is (mathematically) unrelated to the other dark arts of math, the umbral calculus and Bernoulli umbra.
• Arthur, Merlin: These two characters play various games to convince Arthur of true statements. There are complexity classes named Merlin-Arthur and Arthur-Merlin accordingly. They have had recent forays into the quantum world as well.
• Your: The complexity class $P^{TALLY - (NP \cap coNP)}$ has been referred to as “Your Polynomial”. Here the “You” is Scott Aaronson, who felt a need to discuss the class. It has been somewhat retconned to stand for Yaroslav-Percival. Percival was chosen as a friend of Arthur (see Arthur, Merlin), and Yaroslav because, well, a name was needed with a Y. He must be a recent Eastern European immigrant to Camelot.
• Catalysis: A quantum catalyst is a state that permits certain ways of accelerating or improving communnication, despite never being “used up” as a resource - its mere presence helps. The process by which it helps is called catalysis. There is a similar but entirely unrelated notion of catalytic space for Turing machines, and corresponding classes CSPACE and CL.
• Games Against Nature: A certain type of computation with existential and randomized operators allows a computer to play a “game against nature”, with a resulting complexity class called GANSPACE. The relationship to CAHSPACE (Cards Against Huamnity Space) is hitherto unknown, but likely would cause PH to collapse to the third level.
• Oblivious: Certain computations can be done obliviously if their memory access patterns do not depend on the input data. On the practical level, this gives rise to oblivious data structures and transfer protocols. On the theoretical side, there’s oblivious RAM, Turing machines, and corresponding complexity classes. There’s a similar but distinct notion of cache-oblivious algorithms, such as sorting.
• Stoic: Problems can be solved be a stoic algorithm if the accepting and rejecting paths follow certain constraints.
• Platypus: The platypus channel is a particular quantum channel, that is, a model of how quantum data might become corrupted. It has many surprising and counterintutive features, hence the name.
• Pants: A pair of pants is a particular topological manifold-with-boundary which can be used to decompose other, more complicated surfaces. This forms a pair-of-pants decomposition. There are associated pants complexes and hyperbolic pants.

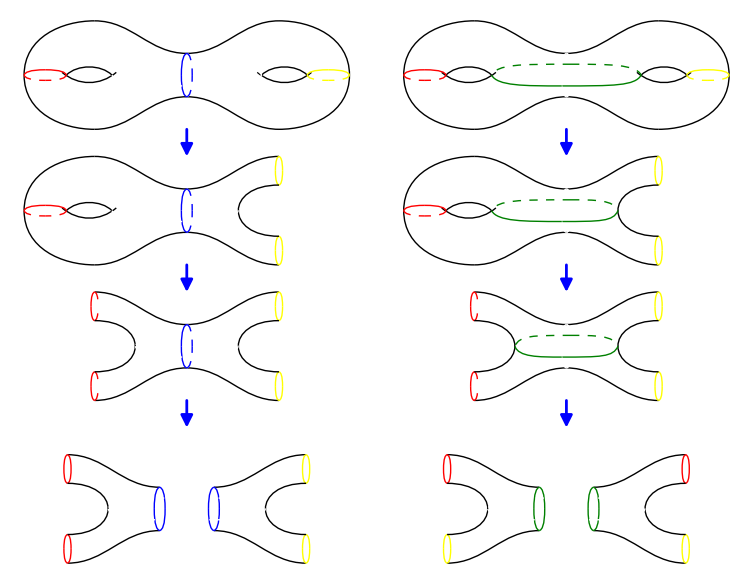Pictured: Two inequivalent pants decompositions.

• Ham Sandwich: The ham sandwich theorem is a statement about equally dividing multiple “substances” (subsets of R^n) in an even way, with a plane. That, intuitively, you can cut a ham sandwich with three ingredients (bread, cheese, and ham) in half, such that each half of the sandwich has half of each ingredient. This is possible with at most three ingredients, because we live in three dimensions. In one dimension, this theorem is the fact a median exists, and in two dimensions, it is known as the “pancake theorem” (that you can cut a pancake to get half of the batter and half of the chocolate chips: two dimensions, two ingredients).
• Banana Man: The Banach analytic manifolds form a category, and the convention for naming categories is to take the first three letters (or, most representative three). For instance, topological spaces are “Top”, and groups are “Grp”. When multiple words are present, they are combined. Under this convention, the category of Banach analytic manifolds are known as “BanAnaMan”. A good argument against picking a shorter abbreviation!
• Pencil: There are several related notions of pencils.
• Chicken McNuggets: The Chicken McNugget theorem states that for any two relatively prime positive integers $m,n$, the greatest integer that cannot be written in the form $am + bn$ for nonnegative integers $a, b$ is $mn-m-n$. So called because it arises from a problem: if a store sells chicken nuggets only in boxes of (say) $m=9$ and $n=20$, what is the smallest order you could not place? The answer is 151, and for any value above 191 there is a way to build your order. In other contexts this is known as the Frobenius Coin problem, and gives rise to the McNugget numbers.
• Pin: The pin group is a certain topological group. The pun is involed. Before the pin group, came the Orthgonal group $O(n)$, and from this was built the Special Orthogonal group $SO(n)$. These had a relationship where $O(n)$ acted like “two copies” of $SO(n)$. Later, physicists worked with the Spin group, $Spin(n)$. Subsequently, it was found that one could take “two copies” in much the same way. Well, if taking two copies of $SO(n)$ was “dropping the S”, the double of $Spin(n)$ should be $Pin(n)$. The name was also intended as a dirty joke on the French word pine, slang for penis.
• Hedgehog: There are hedgehog hypergraphs, a sort of modification of a complete graph where each edge gets turned into a hyperedge with a third vertex - a “spike” of the hedgehog. Similar in spirit but very different in quality is the hedgehog space of topology. Both of these are unrelated to the three(!) other hedgehojbects on this page.
• Shelling Antimatroids are a system for reducing a convex set down to a pseudotriangle.
• Art Gallery: The art gallery problem describes arrangements of observers in a room to protect art. It also makes use of pseudotriangles.
• There is a whole host of math terminology about seed puns. This started with sheaves; a sheaf is traditionally part of wheat. This led to other terms, such as a presheaf or cosheaf; or sheaves that are ideal, reflexive, injective, invertible, or skyscrapers. They can even be flabby or perverse, or soft or fine. But the puns sprouted quickly with stalks, germ – as in wheat germ – and gerb. No relationship to root systems or kernels, although corn may be of interest.
• Motive: It is frequently said that mathematicians study things just for the sake of beauty, but they often have other motives, and their math may be motivic or not.
• Sometimes notation shouldn’t be made into words. The $ \partial \bar \partial$-lemma has unfortunately had its named turned into the ddbar lemma.
• In generalized games of Nim, some positions can be rigid or risky; by considering the f-morphism where you try to make your opponent lose, these become frigid and frisky. This terminology may currently be confined to Chapter 13 of the book “Winning Ways for Your Mathematical Plays, Volume 2” by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy – but it is too good not to mention. (I’m grateful to this redditor and this pdf). Like many of Conway’s works, it is a treasure trove of fun one-off terminology, such as tame, tameable and wild games, loony positions, etc. etc.
• Summer, Winter? The (painfully abstract) notion of dualizing object has earned several other more colorful names. If you wish to be a lawyer like lawvere, they are “objects sitting in two categories”. To be poetic, they are “objects keeping summer and winter homes”. And finally, some people call them “schizophrenic objects”, although this is best avoided and no longer in use.
• Condensation, Liquids: An alternative approach to topology concerns condensed sets. Doing algebra on these sets leads to the study of liquid vector spaces and solid groups.
• • A further alternative to condensed sets are pyknotic sets, from a Greek work for condensation (as opposed to Latin condensio). The process of pyknosis also also occurs in biology, where it is followed by kayorrhexis, or “bursting kernel”; perhaps at some point this will be worked into a long pun involving the kernel of a map and a short exact sequence.
• • The first “major” application of condensed mathematics involved liquid vector spaces and so was termed the liquid tensor experiment, a pun on the musical group Liquid Tension Experiment.
• • Scholze has a number of works on anima. On the face of it, “anima” starts as the synonym of ∞-groupoid, which he says is too unwieldy. He points to “justification” for the name in this paper, where he simply states:

We prefer the term “animated set,” or “anima” for brevity, suggested by the general naming convention: we believe the term “space,” whose origins seem to be historical, to be highly nondescriptive—it is arguable whether something as combinatorial as a simplicial set should count as a space, and also note that “spaces” in the sense of Lurie do not have an underlying set of points. Philosophically, “anima” means something like “soul”—and, indeed, the functor from topological spaces to their homotopy category extracts something like the soul of a space: it only remembers data independent of any worldly representation in terms of physical points.

• • His anima give rise to animated categories and the animation functor.
• Magic, Mana: In quantum mechanics, a certain set of states (Clifford states) are easy to work with, but offer no real power to “do” something quantum on a computer. Magic (1, 2) is a measure of how far a state is from any Clifford state, and thus how much it might defy simple intuition. It is roughly synonymous with the much less fun idea of non-stabilizerness. To create magic, you need a different resource called mana which is another valuable resource.
• Prism: Te field of crystalline cohomology is primarily concerned with prisms. These form prismatic sites. Actually, oppo-sites are defined first in the opposite category, and their categorical dual is then a “site”. Reading this, I find myself need a mug of warm oppoffee.
• High School: A particular set of 11 axioms define an algebraic struture called a high school algebra with one constant symbol (“1”) and three binary operations (+, *, ^). Besides describing natural numbers, they describe a painful thing called a bicartesian closed category. Strictly speaking, they are the axioms of an exponential commutative semiring - one which has a multiplicative identity but not necessarily an additive one.
• Attractor, Strange, Crisis, Shyness: An attractor is the set of points that a dynamical system approaches as limit points. Attractors are strange if they have a fractal structure, and “strange attractors” have been the basis for countless puns about math nerds in romance. An attractor is in crisis if an arbitrarily small perturbation to the parameters of the system causes that attractor to disappear. Shyness is a sort of dynamical-systems-ese for “almost nowhere”, within the space of dynamical systems; the opposite of being shy is being prevalent. It is conjectured but unknown where attractors in crisis are all shy.
• • Several strange attractors have earned their own names. There’s Arnold’s tongue and cat, Hofstadter’s butterfly, a map for bakers kneading dough and a similar one for smiths making horseshoes, and a map that mimics the floating of Tinkerbell.

Particles

Particle physicists like to give some particles amusing names.

• Stop: A stop is a supersymmetric partner particle of a top quark. The convention is to prefix an “s”¹ to the standard name of a particle, e.g. “electron” becomes “selectron”. Stop squarks are important because they would be the lightest supersymmetric particle, and thus the first one found, if supersymmetry were true (it likely is not). Other funny names include “sup” and, if you’re a German speaker, “stau”: “stau” is the German word for “traffic jam”.
• Anyon: Not to be confusion with anions or good ol’ onions, anyons are particles that are neither fermions nor bosons. Since they don’t fit into either class, they can be any-thing else they want to, hence the name! They cannot exist as legitimate particles in a universe with at least three spatial dimensions (like ours), and this is part of the spin-statistics theorem; but they can exist as effective quasiparticles in 2D surfaces. They are often categorized as Abelian or non-abelian anyons. Recently, the term Nonabelion has come into use, although the (decidedly less exciting) “abelion” has not caught on.
• Onium: The unstable particles known as onia are made of a particle and their own antiparticle.
• Glueball: These hypothetical particles consist of many gluons that are “glued” together. Actually, gluon is already a funny word, so named because they “glue” protons and neutrons together – but at this point we’re all largely used to the name, and it’s lost most of its humor.
• Ghosts: These virtual particles simplify certain calculations.
• Skyrmions: Named after Tony Skyrme, these particles have earned a truly bizarre name. They are also known as hedgehog solutions; see below for the related hedgehog theorem.
• Penguins: Penguin diagrams are an important class of interactions in particle physics. They are “one-loop” diagrams, which is the second-simplest kind of interaction – the simplest are “tree-level” diagrams. Usually the tree-level diagrams are the most important, but in some cases – for particular quantities one may care about, such as CP violation – penguin diagrams actually become more important. They are so named simply because they look like a penguin.

Graphs

There are many named graphs of small size. While larger important ones are often simply named after humans who studied them (e.g. “Tutte cage” or “Higman-Sims graph”), small enough ones are just given descriptive names. There are too many to refer to entirely, but some choice ones are:

Paw, Claw, Gem, Jewel, Butterfly (aka Hourglass), Fork (aka Chair), Kite, Dart, House, Bull, Cricket, Cross, “H”, “A”, “R”, “E”, “P” (graphs that look like their respective letters), Banner, Net, Domino, Fish, Antenna, Longhorn, Eiffel Tower, Rising Sun, Parachute, Parapluie.

The letter-named graphs can be remembered by the mnemonic raphe, in the unlikely event that that is a word you know. Sometimes the letter “I” is included to mean the 2-vertex complete graph. There are also some series of graphs with nice names:

Pan, Sun, Star, Triad, Spider, Wheel, Ladder, Ladder Rung, Cocktail Party, Sunlet, Crown, Apple, Bicycle, Building, Fan, Hole, Windmill, Gear, Helm, Web

Then there are classes of graphs, with certain properties. There’s Cactus graphs, Caterpillars, Lobsters, and Cop-win graphs – as in, a cop can beat a robber in a game. Graphs can be slim, slender, or even skeletal. They can be charming, graceful, harmonius, and pretty. They could be good or even perfect. They could even go beyond and be strongly perfect, very strongly perfect, or absolutely perfect. They may be murky. Finally, there are some things they can be that shouldn’t ever have become adjectives: graphs could be coin (which is synonmous with being planar), they might be visibility, or they might just be bip*.

Another important class is the Snarks, including Flower snarks.

Besides the well known terms “cycle”, “path”, and “walk” in a graph, there is the slightly less common “circuit” and the rare trail.

Some graph properties have funny names. While “tree” and “leaf” are pretty common, there’s also arboricity, foliage and foliage partitions.

Some graph properties are evasive. The scorpion graphs showed that there are some interesting highly non-evasive properties, disproving a conjecture.

Curves

People like to name particular curves.

• The limaçon comes from the French word for “snail”, and indeed is sometimes called Pascal’s snail. It comes in four varieties: the convex limaçon, the dimpled limaçon, the looped limaçon, and the cardioid.
• There are various lemniscates, a Latin term meaning “ribbon”, and all resembling the infinity symbol in some form: ∞. Bernoulli, Booth, and Gerono each have their own. Bernoulli’s belong to a larger class called “lemniscates” but looking, in fact, nothing like one. The Devil’s curve (see below) also belongs here.
• Cardioids are so named because they (supposedly) look like hearts, and Nephroids look like kidneys. But Deltoids are not named after the muscle: rather, the curve and the muscle are both named after the Greek letter Delta Δ which they both resemble.
• Cissoids come from a term meaning “ivy-shaped”, while Conchoids mean “shell-shaped” and Strophoids are a “belt with a twist”. A strophoid can also be called a folium, meaning “leaf”.
• • Unfortunately, the folium of Descartes is not a folium, and the conchoid of de Sluze is not a conchoid. But they both are cissoids, and the conchoid of de Sluze is also a strophoid.
• Astroids are similar to deltoids but with one extra point, and resemble stars. It is also known as a tetracuspid, but it is nothing like two copies of the Bicuspid, which resembles a tooth.
• Devils persist in bother mathematicians with their pathologies, and so earn their share of eponyms. They have a curve and a staircase. They also have their own dice, mostly marketed as a game, but with interesting mathematical considerations too.
• There is also a Witch of Agnesi. It is not as troublesome as the name suggests: it was a mistranslation when the Italitan averisera (“versed sine curve,” from the Latin vertere, “to turn”) was mistaken for avversiera (“witch” or “wife of the devil”).
• There are two Butterfly curves: one trascendental and one algebraic. As far as I know, they have no applications or particularly interesting properties besides being appealing to the eye.
• Hedgehogs get their own curve as well. Perhaps a favorite animal of mathematicians, perhaps simply notable for being spiky.
• Wittgenstein’s rod might belong in the “dirty jokes” section, but is funny name even without any obscene connotation. Oddly, the curve looks nothing like a rod: the rod is the bar used to create the curve. And yet, the curve is called the rot.
• Caustic curves earned their name because they can focus sunlight to burn something.
• Glisettes, from the French word glisser “to slip”, describe curves from line segments sliding along two others. Roulettes are similar an opposite: they are defined in terms of rolling without slipping!
• Curves have envelopes, and you can evolve or involve them. Confusingly, the in-volute is also known as the e-volvent.
• Pedal curves were originally about the paths of pedals on a vehicle. They have negative pedal curves and contrapedal curves as two different opposites.
• Curve terminology is full of Grecoroman terminology with wonderful endings and plurals. A directrix, or dirigent, goes with a generatrix, or describent, and isn’t to be confused with an indicatrix. Several of them are directrices, generatrices, and indicatrices.

Knot

• Knots can be wild or tame.
• The stevedore knot is named after the old profession of stevedore, another name for dockworker.
• Knots have a writhe as an important invariant. The standard notation for this is Wr, unfortunately also the notation for a wreath product of groups. Knots also obey skein relations.
• Knot theorists love to take nouns and make them into adjectives. Knots can be pretzel, twist, slice (including topologically slice or smoothly slice), or ribbon, among others. The phrase “a ribbon knot” doesn’t sound too strange, because we easily parse “ribbon knot” as a compound noun in English. But other sentences sound bizarre: “If a knot is smoothly slice, is it necessarily ribbon?”. This example is known as the slice-ribbon conjecture. This conjecture is open, but is known to be true for everything pretzel!
• Some surfaces are open books. These books have a binding and several pages. If a knot is a binding, it is fibered.

Surfaces

Some surfaces are mentioned in other places on the page (like Labs septic or the Klein bottle).

• The Saddle tower indeed consists of many saddles but would be very difficult to adapt for horse riding. A Monkey saddle is much more practical – as long as are a monkey, or otherwise have a tail.
• Continuing the trend of useless household objects, Whitney umbrellas do a poor job of catching rain, but a good job of describing singularities in string theory.
• Oloids were apparently named just for being a funny curved surface in the same vein as paraboloid, hyperboloid, and so on – but I can’t find a source. Visually it is extremely similar to a . Wiktionary says this should be pluralized as sphericons*, but I have to believe this should be spherica. Spherica have a pleasant rolling motion, while oloids lay flat.
• Rolling on, a gömböc is a 3-dimensional object that will always roll to a single equilibrium. They were only proven to exist in 2006, but now anyone can 3D print one as a little desk toy.

• A thin homoeoid and thin focaloid are both identical, as surfaces, to ellipsoids, but they define different densities on the surface. This is awful.
• Catenoids and helicoids are the only two minimal surfaces (zero mean curvature) that are also surfaces of revolution. If “zero mean curvature” is relaxed to “constant mean curvature”, then there are also unduloids and nodoids. This list is exhaustive, except for the degenerate cases of plane, cylinder, and sphere.
• • The Double bubble theorem also concerns surfaces of constant mean curvature, and shows that they take a certain form of two soap bubbles.
• The umbilical points of a surface resemble (…in principle…) a navel, where an umbilical cord attaches. I fail to see it. It’s an open problem whether they always exist.
• Bagpipes turn out to classify even some quite pathological connected surfaces.
• A rational, normal scroll is a projective ruled surface. “Scroll” is an old term for ruled surface.
• The superegg is a three-dimensional version of a superellipse, and is particular type of superellipsoid. In 2D, there are squircles – the serious and formal name for a squround.

Surnames

Sometimes a name is funny not deliberately, but because it is named after someone whose name was already a word. How funny or surprising this can be is entirely dependent on how familiar the name is a word vs as a name. For instance, most native English speakers will not think “Taylor polynomial”, “Smith number”, or “Stone duality” sound funny, even though “tailor”, “smith”, and “stone” are all words (each of them a noun and verb!). My bias here in terms of what I find funny is certainly a function of what languages I know and how well. Please email me with suggestions!

• A Knödel graph is a particular class of graphs suggested by W. Knödel in 1975 to model gossiping. “Knödel” is the German for dumpling. Coincidentally, but the Hungarian word for a Knodel is “gombóc”, from which the mathematical term “Gömböc” is derived, see above. It’s entirely reasonable to say that the funnier name from W. Knödel’s 1975 paper is the problem he studied, which has become known as the gossiping problem or gossiping process.

Pictured: A bipartite Knödel grap

• Felix Klein has several objects, such as Klein bottles and two different Klein surfaces, named after him. “Klein” is German for “small”. This is the source of frequent puns in German, where Klein bottles are criticized for being “too small to hold anything”, a reference to their zero-volume interior. Klein bottle was already a mistake: in German, the name was “Klein Fläche”, meaning “a Klein surface” (no relation to the other two). A translator misread “Fläche” and “Flasche”, meaning “bottle”, believing it to be a reference to the apparent bottle-like shape. The English name stuck. It is now known as “Flasche” (or something “Schlauch”) in German too.
• Labs septic sounds like an issue with a chemical spill, but is actually a surface named after Oliver Labs, and is a septic curve (a curve of order 7), not a sewage system.
• There are many Haar objects in math, such as Haar measure and Haar graphs, named after the Hungarian mathematician Alfréd Haar. The surname “Haar” means “cold sea fog” in English and Scots; “hair” (of one’s head) in German, Dutch, and Afrikaans; and “hare” (rabbit) in Middle English.
• A Poisson process or distribution is named after Siméon Denis Poisson. His name “poisson” means “fish” in French. This has been used for puns before, e.g. the Poisson process in this video is generated by an actual goldfish. (Skip to 5:17.)
• Frucht graphs are named after Robert Frucht. The name “Frucht” is German for “fruit”.
• Heyting algebras are not for people who hate algebras. They are named for Arend Heyting. There is a similar joke where a knot theorist asks a young student what branch of math and sciences they enjoy. The student, who aspires to be an engineer, replies: “well… not theory”. The professor is delighted.
• Killing fields and Killing forms are named after Wilhelm Killing. Wikipedia suggests that Killing fields are sometimes known simply as “Killings”, which I hope is not very true.
• A Boy’s surface is appropriate for all ages!
• Peano axioms describes all natural numbers, not just the first 88.
• There are a few Valiant languages, named after Leslie Valiant.
• A Griess algebra tells you nothing about slippery oil. It doesn’t even tell you anything about semolina.
• The Leech lattice won’t leave you with bite marks, but it is full of deep holes. It provides optimal solutions to many kissing number problems as well.
• As irony would have it, the Held group is an abstract object, and has never once been hugged.
• You may have heard of cousin primes, so-called because they’re close (only four apart) but not as close as twin primes. So you may think that Cousin problems are similar, but no, they are just named after Pierre Cousin.
• Lie groups and algebras are not lies. Note that the name “Lie” is pronounced like “Lee” – pronouncing it as “lye” is an excellent way for a student to out themselves.

Some names are only “schoolboy funny”.

• There are Dyck words** which make up the Dyck language.
• The Cox-Zucker machine was deliberately named for this purpose.
• Jacques Tits has a group, an alternative, a metric, an index, a cone, and a system with his name on them.
• Of no relation, the Tarski indefinability theorem is sometimes referred as the TIT.
• There are Kummer surfaces and associated Kummer varieties and Kummer configurations, as well as many other objects bearing his name.
• The Wiener process generates a Wiener sausage. The latter is a deliberate pun on Viennese sausage (“Wiener” is German for “Viennese”).
• The Fokker-Planck equation for particle distribution bears no connection to the Fokker periodicity block for scale tuning theory except for the namesake, Adriaan Fokker.
• A Wick rotation could be pleasant or very painful, depending on the angular velocity.
• Many objects bear name Hardy-Littlewood, such as their maximal functions, their zeta-function conjectures, or their circle method to name just a few.

Dirtier jokes

• The language WPP also known as Wide PP was poor choice. Its even naughtier cousin is the Length-dependent Wide PP.
• The hairy ball theorem states that there is no nonzero tangent vector field on a sphere (or any sphere in an even number of dimensions). So called because it can be summed up as “you can’t comb a hairy ball flat”. In Europe it has earned the affectionate name of the hedgehog theorem.

1. One would think that the “s” in a particle name stands for “super-“ or “symmetric partner”. Wikipedia claims that the s actually stands for “scalar”, because the particles are spin-0 and therefore scalar fields. I’m skeptical, and can’t find a citation. Bosons get a different naming convention, where the final “-on” is changed to “-ino”, e.g. photino. ↩